【Python】機械学習のPCA(主成分分析)で次元削減する方法を解説

今回は、機械学習の次元削減において最も有名な手法であるPCA(主成分分析)について紹介します。

PCAの概要およびPythonを使用し、PCAを実装する方法を解説していきます。

動画で詳しく学習したい方はこちらもおすすめ

次元削減とは

次元削減とは、高次元データの特徴量を減らすことで解析を簡素化する手法です。

次元削減をすることで、計算コストの低減、データの可視化が可能です。

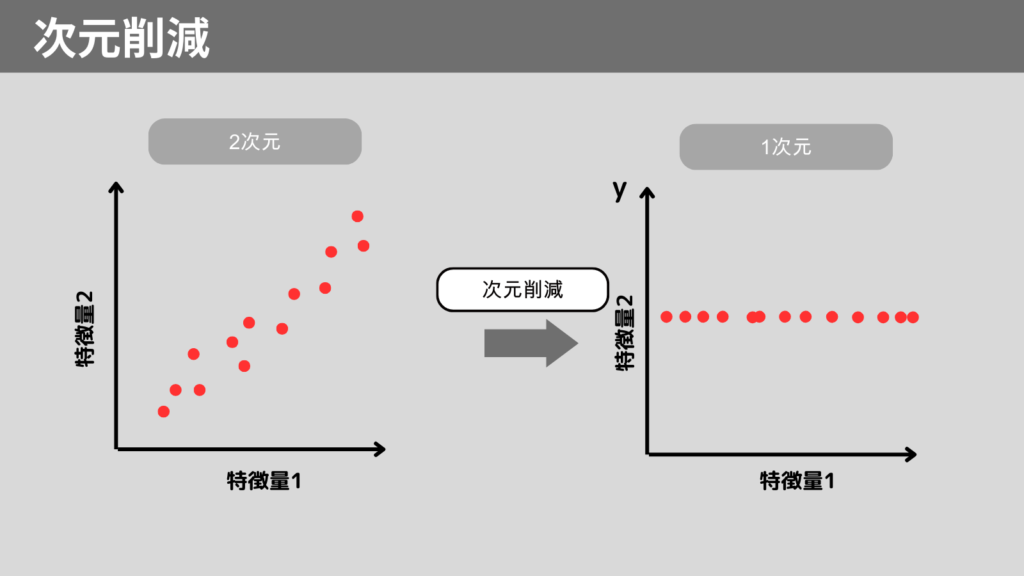
次元削減の代表的な手法

次元削減の代表的な手法は以下の通りです。

今回は上記の手法から有名なPCAについて説明していきます。

PCA(主成分分析)とは

PCA(Principal Component Analysis)は、最も有名な次元削減の手法です。

PCAはデータの分布を調べ、データが分散している方向を見つけます。

この方向を「主成分」と呼びます。

PCAはこの主成分を見つけ、データをその方向に投影して次元を削減します。

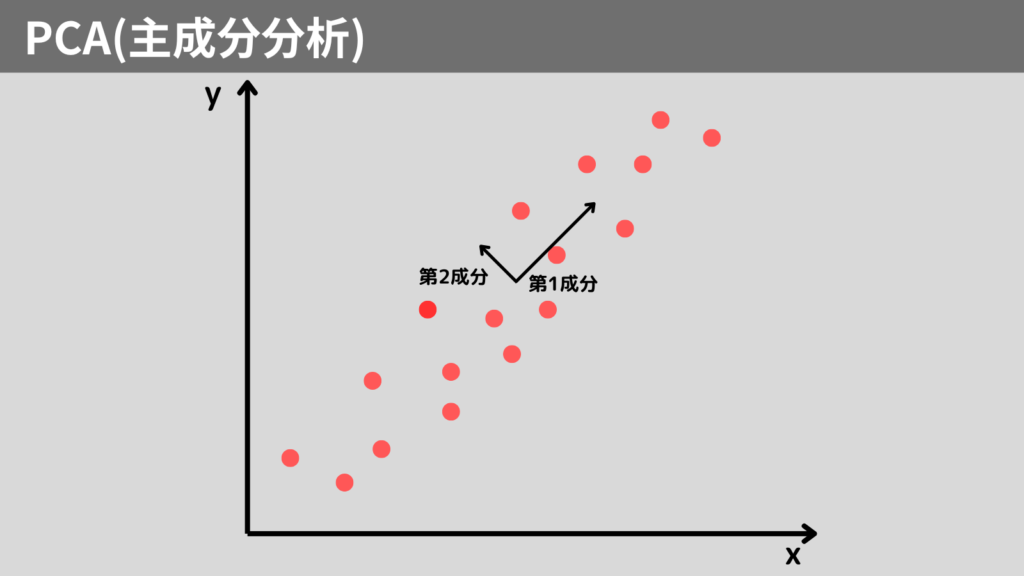
PCAの目的

PCAを行う目的は主に以下です。

Python実践 PCA

それではPythonを使用し、PCAを実装してみましょう！ scikit-learnライブラリを使用します。

使い方は以下の通りです。

n_componentsで次元削減後の次元数を指定します。上記では2次元データに次元削除した例です。

fit_transformで構築したPCAのモデルをデータXに適応します。

サンプルコードは以下の通りです。

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# データセットの読み込み
data = load_iris()
X = data.data  # 特徴量データ
y = data.target  # クラスラベル

# データの標準化
scaler = StandardScaler()
X_standardized = scaler.fit_transform(X)

# PCAの適用(2次元)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_standardized)

# 結果のプロット
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k', alpha=0.7)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA: Iris Dataset')
plt.show()

実行結果

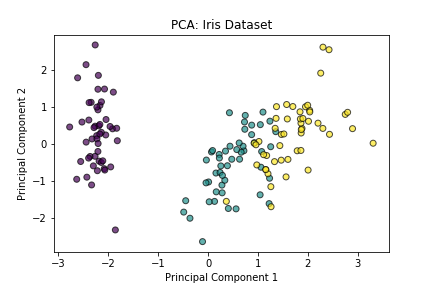
実際にPCAを実装するときは、事前にデータを標準化しておく必要があります。

各特徴量を同じスケールにすることで、データの偏りを減らすことができます。

まとめ

機械学習における次元削減のなかでも有名な手法であるPCA(主成分分析)について紹介しました。

PCAはデータの分散を最大化する方向(主成分)を見つけ、データをその方向に投影して次元を削減します。

PCAをPythonで実装する方法は以下の通りです。

また、事前に各特徴量を標準化しておく必要があることに注意してください。

ここまで読んでくださりありがとうございます。