【Python】機械学習のNMF(非負値行列因子分解)で次元削減する方法を解説

今回は、機械学習における次元削減の手法のひとつである、NMF(非負値行列因子分解)について解説します。

NMFの特徴、Pythonを使用し、NMFを実装する方法を紹介していきます。

動画で詳しく学習したい方はこちらもおすすめ

次元削減とは

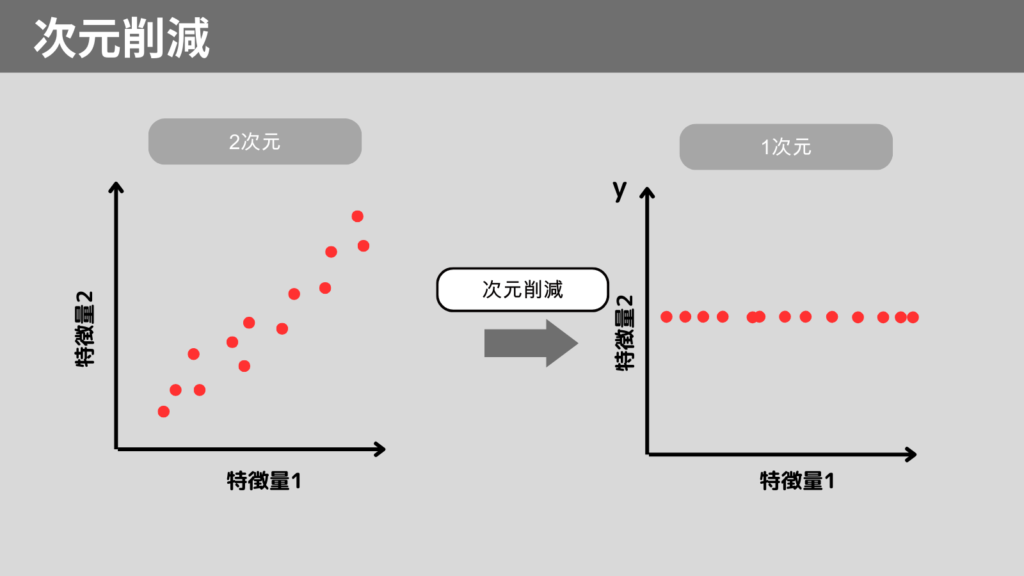
次元削減とは、高次元データの特徴量を減らすことで解析を簡素化する手法です。

次元削減をすることで、計算コストの低減、データの可視化が可能です。

次元削減の代表的な手法

次元削減の代表的な手法は以下の通りです。

今回は、上記の手法からNMF(非負値行列因子分解)について説明していきます。

NMF(非負値行列因子分解)とは

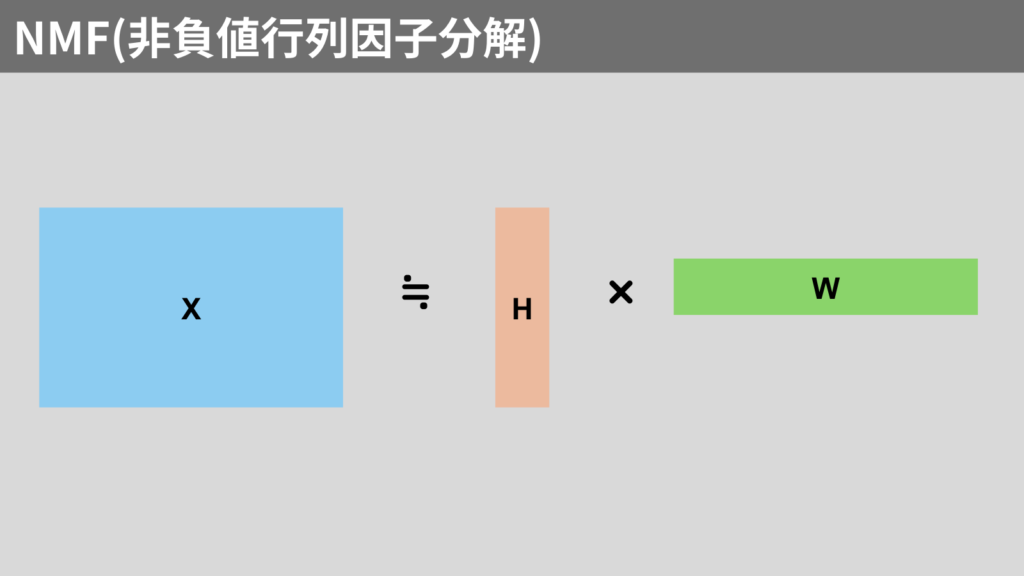
NMF(Nonnegative Matrix Factorization)とは、非負値(正の値)を持つ行列を解析する手法です。

以下の図のように行列を分解します。

非負値なデータには、画像データなどがあります。

NMFのメリット

NMFを使用するメリットは以下の通りです。

データが非負値であるという制約はありますが、非負値であるがゆえに効率的に計算可能です。

Python実践 NMF

それではPythonを使用し、NMFを実装してみましょう！

scikit-learnライブラリを使用します。

使い方は以下の通りです。

n_componentsで次元削減後の次元数を指定します。上記では2次元データに次元削除した例です。

fit_transformで構築したNMFのモデルをデータXに適応します。

サンプルコードは以下の通りです。

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import NMF
import matplotlib.pyplot as plt

# データセットの取得
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape

# データの準備
X = people.data

# NMFの適用
nmf = NMF(n_components=15, random_state=0)
X_nmf = nmf.fit_transform(X)

# NMFで得られた基底画像をプロット
fig, axes = plt.subplots(3, 5, figsize=(15, 8), subplot_kw={'xticks': (), 'yticks': ()})
for i, ax in enumerate(axes.ravel()):
        ax.imshow(nmf.components_[i].reshape(image_shape), cmap='gray')
        ax.set_title(f'Component {i+1}')

plt.show()

実行結果

まとめ

機械学習における次元削減の手法のひとつである、NMF(非負値行列因子分解)を紹介しました。

NMFは、非負値を持つ行列を解析する手法で、画像データの解析などに用いられます。

NMFをPythonで実装する方法は以下の通りです。

ここまで読んでくださりありがとうございます。