今回はディープラーニングの「損失関数」について解説します。
損失関数とはなにか、代表的な損失関数をわかりやすく説明していきます。
Pythonを使用し、損失関数を実装する方法をあわせて解説します。
動画で詳しく学習したい方はこちらもおすすめ
損失関数とは
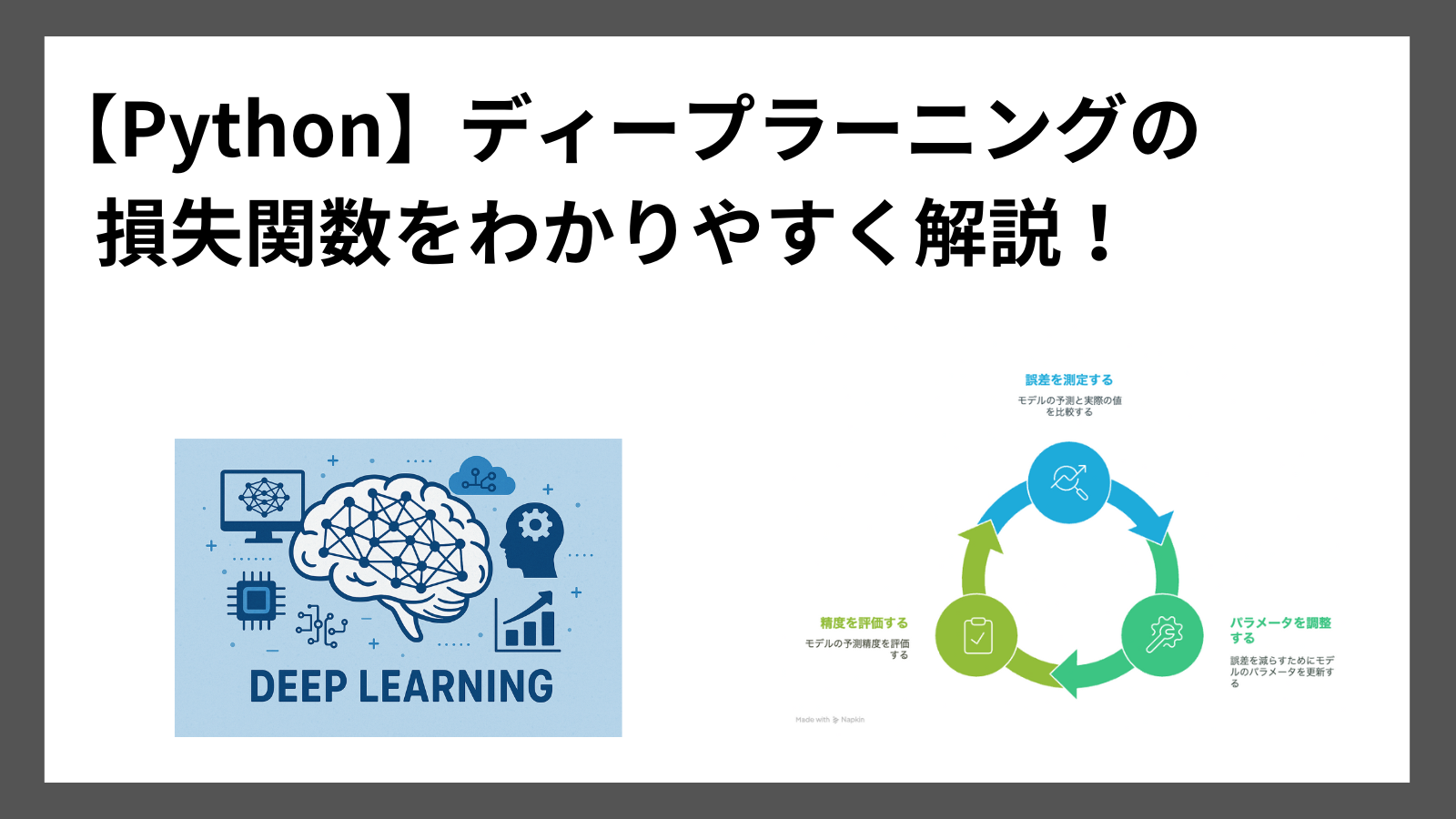
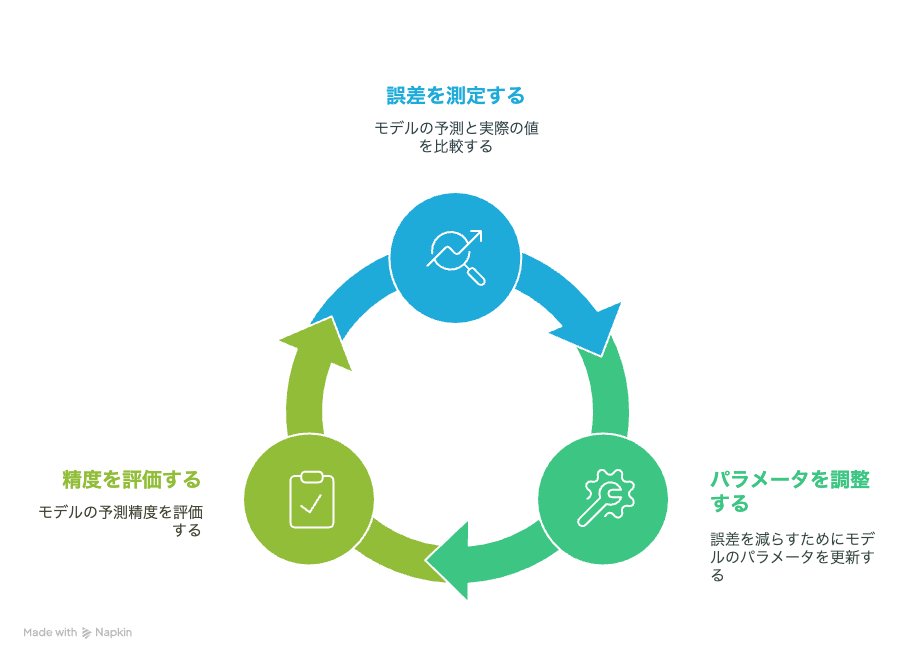
損失関数とは、モデルの予測と実際の値との誤差を数値化する関数です。
誤差が小さくなるように、モデルはパラメータを調整していきます。
モデルの予測精度が高いかどうかの判定に使用されます。
代表的な損失関数
損失関数はいくつか種類があります。その中でも代表的は損失関数は以下です。
- 二乗和誤差
- 交差エントロピー誤差
それぞれの損失関数ついて詳しく説明していきます。
二乗和誤差(SSE)
二乗和誤差(SSE: Sum of Squared Errors)は、回帰問題に使用される損失関数です。
予測値と正解値の差を二乗し、合計する関数です。
二乗するため、誤差が大きい外れ値などの影響を受けやすいという特徴があります。
式は以下の通りです。
$$ SSE = \sum^{n}_{i}(y_i – t_i)^{2} $$
\(y\): 予測値 \(t\) : 正解値 \(n\): データの総数
交差エントロピー(Cross-Entropy)
交差エントロピー(Cross-Entropy)は、分類問題に使用される損失関数です。
予測確率と正解値のズレを数値化する関数です。
$$ E = -\sum^{n}_{i} t_i\log y_i $$
\(y\): 予測値 \(t\) : 正解値 \(n\): データの総数
損失関数の使い分け
二乗和誤差と交差エントロピーは問題の種類によって使い分けます。
使い分け方は以下の通りです。
| 問題の種類 | 損失関数 |
|---|---|
| 回帰 | 二乗和誤差(SSE) |
| 分類 | 交差エントロピー |
Python実践 損失関数
それでは損失関数をPythonを使用し、実装する方法を紹介します。
Python実践 二乗和誤差
二乗和誤差をPythonで実装してみましょう!
自作で二乗和誤差を求める関数を作成します。
import numpy as np
def sum_squared_error(y_true, y_pred):
return np.sum((y_true - y_pred) ** 2)
# 例
y_true = np.array([3.0, -0.5, 2.0, 7.0])
y_pred = np.array([2.5, 0.0, 2.0, 8.0])
sse = sse(y_true, y_pred)
print("SSE:", sse)実行結果
SSE: 1.5Python実践 交差エントロピー
交差エントロピーをPythonで実装してみましょう!
自作で交差エントロピーを求める関数を作成します。
def cross_entropy_error(y_true, y_pred):
return -np.sum(y_true * np.log(y_pred))
# one-hot 表現
y_true_cat = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
y_pred_cat = np.array([[0.9, 0.05, 0.05],
[0.1, 0.8, 0.1],
[0.2, 0.2, 0.6]])
cross_entropy = categorical_cross_entropy(y_true_cat, y_pred_cat)
print("Categorical Cross Entropy:", cross_entropy)
実行結果
Categorical Cross Entropy: 0.8393296907380268まとめ
損失関数について紹介しました。
損失関数は、モデルの予測値と正解値の誤差を数値化する関数です。
モデルはこの誤差を小さくするようにパラメータを調整します。
代表的な損失関数は以下の2つです。
- 二乗和誤差
- 交差エントロピー誤差
それぞれの損失関数はPythonで簡単に実装できることを説明しました。
ここまで読んでくださりありがとうございます。