統計学において重要な手法である仮説検定について、その基本的な概念と実践方法を紹介します。
仮説検定の基本概念
仮説検定の流れ
- 仮説の設定:帰無仮説と対立仮説を設定
- データ収集:試験や実験のデータを収集
- 検定統計量の計算:検定統計量(t値、z値、\(\chi^2\)値など)を計算
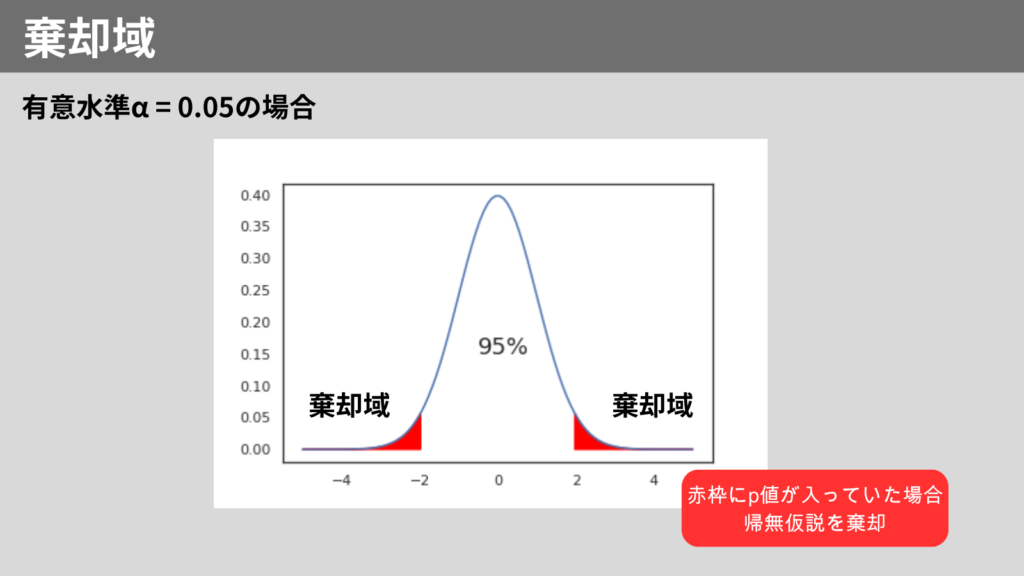
- 有意水準の設定:通常、有意水準α = 0.05を設定
- 判断:
– p値が有意水準以上の場合:帰無仮説を棄却できない
– p値が有意水準未満の場合:帰無仮説を棄却し、対立仮説を支持
帰無仮説と対立仮説
- 帰無仮説:特定の条件や効果が存在しない、または差がないとする仮説
例)新しい教育方法は従来の方法と学力向上に違いがない - 対立仮説:特定の条件や効果が存在する、または差があるとする仮説
例)新しい教育方法は従来の方法よりも学力を向上させる
対立仮説に、研究者が証明したい仮説を設定します。仮説検定では、帰無仮説が成立しないことを示すことで、間接的に対立仮説を支持します。
検定統計量
検定統計量は、帰無仮説の妥当性を評価するために計算される値です。主な検定統計量には以下があります。
- z検定(z値):標本が大きい場合に使用
- t検定(t値):標本が小さい場合に使用
- カイ二乗検定(\(\chi^2\)値):カテゴリデータを検定する場合に使用
有意水準
有意水準は、帰無仮説を棄却するための基準となる確率です。一般的に0.05(5%)が使用されます。
これは、帰無仮説が正しいにもかかわらず、誤って棄却してしまう確率(第一種の過誤)を5%まで許容することを意味します。
p値(p-value)
p値は、帰無仮説が正しいと仮定した場合に、観測されたデータ(またはそれ以上に極端なデータ)が得られる確率です。
p値が設定した有意水準よりも小さい場合、帰無仮説を棄却し、対立仮説を支持します。
Pythonを使ったz検定の実践
ここでは、Pythonを使用して比率の差の検定(z検定)を行います。
例題
ある薬の効果を検証する実験を考えます:
– グループA(新薬投与):100人中45人が改善
– グループB(既存薬投与):120人中30人が改善
仮説:
– 帰無仮説:新薬と既存薬の効果に差はない
– 対立仮説:新薬と既存薬の効果は異なる
import numpy as np
from statsmodels.stats.proportion import proportions_ztest
# データの設定
success_counts = np.array([45, 30])
n_obs = np.array([100, 120])
# z検定の実行
z_stat, p_value = proportions_ztest(success_counts, n_obs, alternative='two-sided')
# 結果表示
print(f'z値: {z_stat:.3f}')
print(f'p値: {p_value:.3f}')コードの説明
- 必要なライブラリをインポートします。
- 各グループの成功数と総数を配列として設定します。
proportions_ztest関数を使用してz検定を実行します。alternative='two-sided'は両側検定を指定します。- 得られたz値とp値を小数点以下3桁まで表示します。
実行結果
z値: 3.116
p値: 0.002p値(0.002)が有意水準(0.05)より小さいため、帰無仮説を棄却し、対立仮説を採用します。
つまり、新薬と既存薬の効果には統計的に有意な差があると結論づけられます。
まとめ
仮説検定は、データに基づいて科学的な結論を導き出すための重要な統計手法です。
本記事では、仮説検定の基本概念と、Pythonを使った実践方法を紹介しました。
統計分析の初心者にとって、仮説検定の概念を理解し、実際にデータ分析に適用することは大きな一歩です。
今回学んだ内容を基に、さまざまなデータセットや研究課題に仮説検定を適用してみることをおすすめします。
ここまで読んでくださりありがとうございます。
参考
おすすめ教材
米国データサイエンティストが教える統計学超入門講座【Pythonで実践】他のUdemyの講座が気になる方はこちら