t検定は2つの集団の平均値を比較するために使用される手法です。
t検定の基本概念、種類、適用場面、そしてPythonを使用した実践例を紹介します。
t検定とは
t検定は、2つの集団の平均値に有意な差があるかどうかを判断するための仮説検定のひとつです。
特にサンプルサイズが小さい場合に適しています。
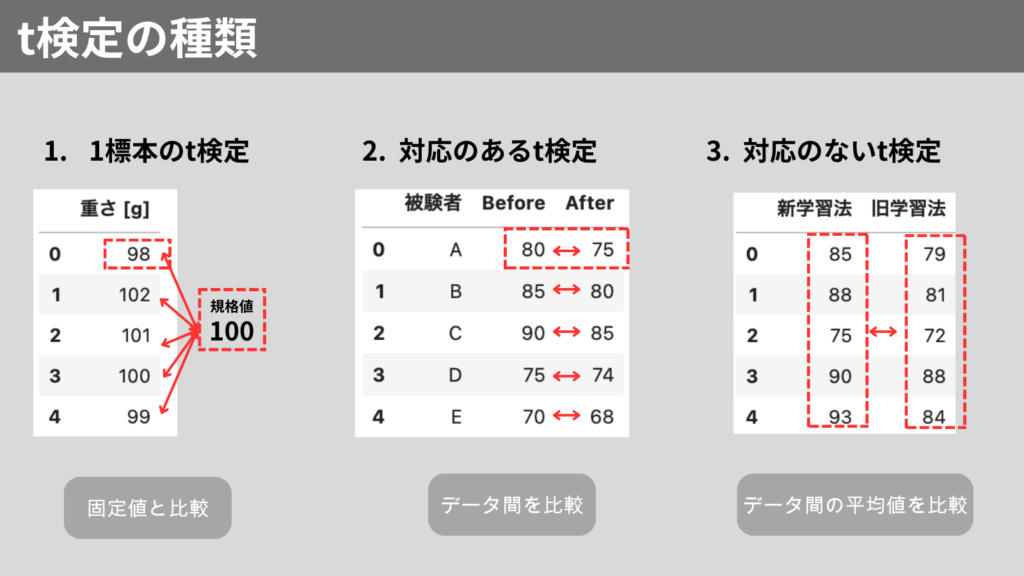
t検定の種類
t検定は主に以下の3種類あります。
- 1標本のt検定
– 1つの集団の平均を固定値と比較
例)ある工場の製品の重量が規格(100g)と異なるかどうか - 対応のあるt検定
– 同じ集団の前後や2つの条件下での平均を比較
例)ダイエット前後の体重の比較 - 対応のないt検定
– 2つの独立した集団の平均を比較
例)男性と女性のテストスコアの平均値を比較
Pythonを使ったt検定の実践
それでは実際にPythonを使用し、t検定をしてみましょう!
1標本のt検定
Pythonを使用し、1標本のt検定を実施する方法を紹介します。
以下を例題にして、サンプルコードを記載します。
例題
ある工場の製品の重量が規格(100g)と異なるかどうか
この場合、以下仮説を設定します。
- 帰無仮説: 製品の重量が100gである
- 対立仮説: 製品の重量が100gでない
import numpy as np
from scipy import stats
# データ:10個の製品の重量(グラム)
weights = np.array([98, 102, 101, 100, 99, 101, 102, 98, 99, 101])
# 1標本のt検定
t_stat, p_value = stats.ttest_1samp(weights, popmean=100)
# t検定の結果を出力
print(f"t値: {t_stat:.4f}")
print(f"p値: {p_value:.4f}")実行結果
t値: 0.2075
p値: 0.8402この結果、p値が有意水準(0.05)よりも大きいので、帰無仮説は棄却できません。
すなわち、対立仮説である製品の重量が100gでないとは言えないことがわかります。
対応のあるt検定
続いては、対応のあるt検定についてです。
以下を例題にして、サンプルコードを記載します。
例題
ダイエット前後に体重に変化があったか
この場合、以下仮説を設定します。
- 帰無仮説: ダイエット前後で体重に差がない
- 対立仮説: ダイエット前後で体重に差がある
import numpy as np
from scipy import stats
# ダイエット前後のデータ(グラム)
before_diet = np.array([80, 85, 90, 75, 70, 95, 88, 82, 78, 77])
after_diet = np.array([75, 80, 85, 74, 68, 92, 83, 79, 75, 76])
# 対応のあるt検定を実行
t_stat, p_value = stats.ttest_rel(before_diet, after_diet)
# 結果の表示
print(f"t値: {t_stat:.4f}")
print(f"p値: {p_value:.4f}")実行結果
t値: 6.3772
p値: 0.0001この結果、p値が有意水準(0.05)よりも小さいので、帰無仮説を棄却します。
つまり、対立仮説である「ダイエット前後で体重に差がある」を支持します。
対応のないt検定
最後に、対応のないt検定です。
以下を例題にして、サンプルコードを記載します。
例題
新しい学習アプリを使ったグループと従来の学習方法を使ったグループのテスト結果の比較
この場合、以下仮説を設定します。
- 帰無仮説: 新しい学習アプリを使ったグループと従来の学習方法を使ったグループのテスト結果の平均に差がない
- 対立仮説: 新しい学習アプリを使ったグループと従来の学習方法を使ったグループのテスト結果の平均に差がある
import numpy as np
from scipy import stats
# 新しい学習アプリを使ったグループのテスト結果
app_group = np.array([85, 88, 75, 90, 93, 82, 86, 78, 91, 89])
# 従来の学習方法を使ったグループのテスト結果
traditional_group = np.array([79, 81, 72, 88, 84, 76, 80, 77, 85, 82])
# 対応のないt検定の実行
t_stat, p_value = stats.ttest_ind(app_group, traditional_group)
print(f"t値: {t_stat:.4f}")
print(f"p値: {p_value:.4f}")実行結果
t値: 2.2430
p値: 0.0377この結果p値が有意水準(0.05)よりも小さいので、帰無仮説を棄却します。
つまり、対立仮説である「新しい学習アプリを使ったグループと従来の学習方法を使ったグループのテスト結果の平均に差がある」を支持します。
まとめ
今回t検定の基本概念、種類を紹介しました。
t検定は仮説検定の基本です。
t検定をマスターすれば、データ分析力は大きく上昇します!
ぜひ、マスターできるようになってください!
ここまで読んでくださりありがとうございます。
参考
おすすめ教材
米国データサイエンティストが教える統計学超入門講座【Pythonで実践】他のUdemyの講座が気になる方はこちら