今回は、データの正規性を評価するために使用する、シャピロウィルク検定とQ-Qプロットについて解説します。
動画で詳しく学習したい方はこちらもおすすめ
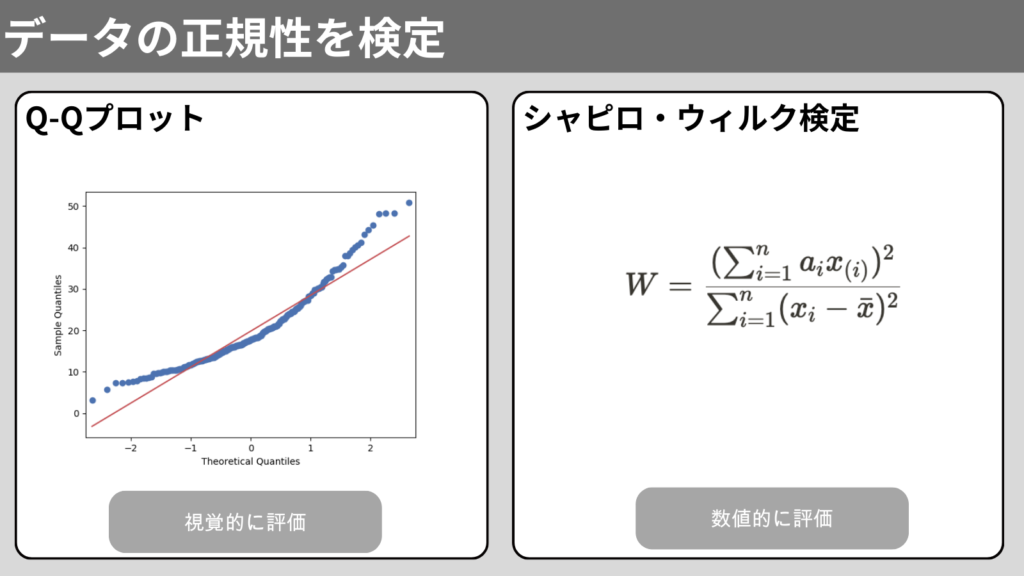
シャピロ・ウィルク検定とは
シャピロ・ウィルク検定(Shapiro-Wilk test)は、データの正規性を評価するための検定です。
言い換えると、データが正規分布に従っているかを評価します。
統計学において、データが正規分布に従っているかは重要です。
様々な検定方法がデータが正規分布に従っていることを前提にしているからです。
なので、分析を始める前にデータが正規分布に従っているかを確認することが大切です。
シャピロ・ウィルク検定の際は、正規分布に従っているいるかを評価するため、以下仮説を設定します。
- 帰無仮説 : 母集団が正規分布である
- 対立仮説: 母集団が正規分布ではない
つまり、p値と検定結果の関係は以下の通りです。
- p値 > 0.05:帰無仮説を棄却できない(データは正規分布に従う可能性が高い)
- p値 ≤ 0.05:帰無仮説を棄却(データは正規分布に従わない可能性が高い)
Q-Qプロット
視覚的にデータが正規分布に従っているかを評価する方法もあります。
それが、Q-Qプロットです。
Q-Qプロットは、グラフを使って評価します。
データが理論的な分布に従っている場合は、プロットは直線になります。
プロットが直線に近づいていれば、データが正規分布に従っているといえます。
Pythonで正規性の評価
それではPythonで正規性を評価してみましょう!
Pythonでシャピロ・ウィルク検定実践
まずは、シャピロ・ウィルク検定をPythonで実践してみましょう!
seabornのtipsのデータセットを使用します。
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
# tipsデータセットの読み込み
tips = sns.load_dataset("tips")
# 総額(total_bill)に対してシャピロウィルク検定を実施
statistic, p_value = stats.shapiro(tips['total_bill'])
print("総額(total_bill)のシャピロ・ウィルク検定結果:")
print(f"統計量: {statistic:.4f}")
print(f"p値: {p_value:.4f}")実行結果
総額(total_bill)のシャピロ・ウィルク検定結果:
統計量: 0.9197
p値: 0.0000この結果からp値が有意水準(0.05)より小さいので、帰無仮説を棄却します。
つまり、母集団は正規分布に従わないことがいえます。
PythonでQ-Qプロット実践
続いては、Q-QプロットをPythonで実践してみましょう!
シャピロ・ウィルク検定でtotal_billのデータが正規分布に従わないことがわかりました。
そこで、Q-Qプロットで視覚的にみてみます。
Q-Qプロットを描画するには、statsmodelsのapi.qqplotを使用します。
from statsmodels.api import qqplot
# Q-Qプロットを描画
fig = qqplot(tips['total_bill'], line='r')実行結果
qqplot()の引数の説明は以下です。
第1引数: データ
第2引数: line=’r’ regression(回帰)を表示
Q-Qプロットのグラフを見ると、プロットが直線に従っていないことがわかります。
つまり、プロットしたデータが正規分布に従わないことが視覚的にわかります。
まとめ
今回はデータの正規性を検定する方法を紹介しました。
Q-Qプロットで視覚的に正規性を評価し、
シャピロ・ウィルク検定で具体的にどれくらい正規分布に従っているかを確認します。
ここまで読んでくださりありがとうございます。
参考
おすすめ教材
米国データサイエンティストが教える統計学超入門講座【Pythonで実践】他のUdemyの講座が気になる方はこちら