今回はディープラーニングを学習していると、必ず登場する「誤差逆伝播法」について解説します。
誤差逆伝播法は、理解が少し難しいかと思いますが、ディープラーニングの仕組みを理解する上で重要になります。
また、具体的にイメージしやすいようにPythonで「誤差逆伝播法」を実装する方法も合わせて紹介していきます。
動画で詳しく学習したい方はこちらもおすすめ
誤差逆伝播法とは
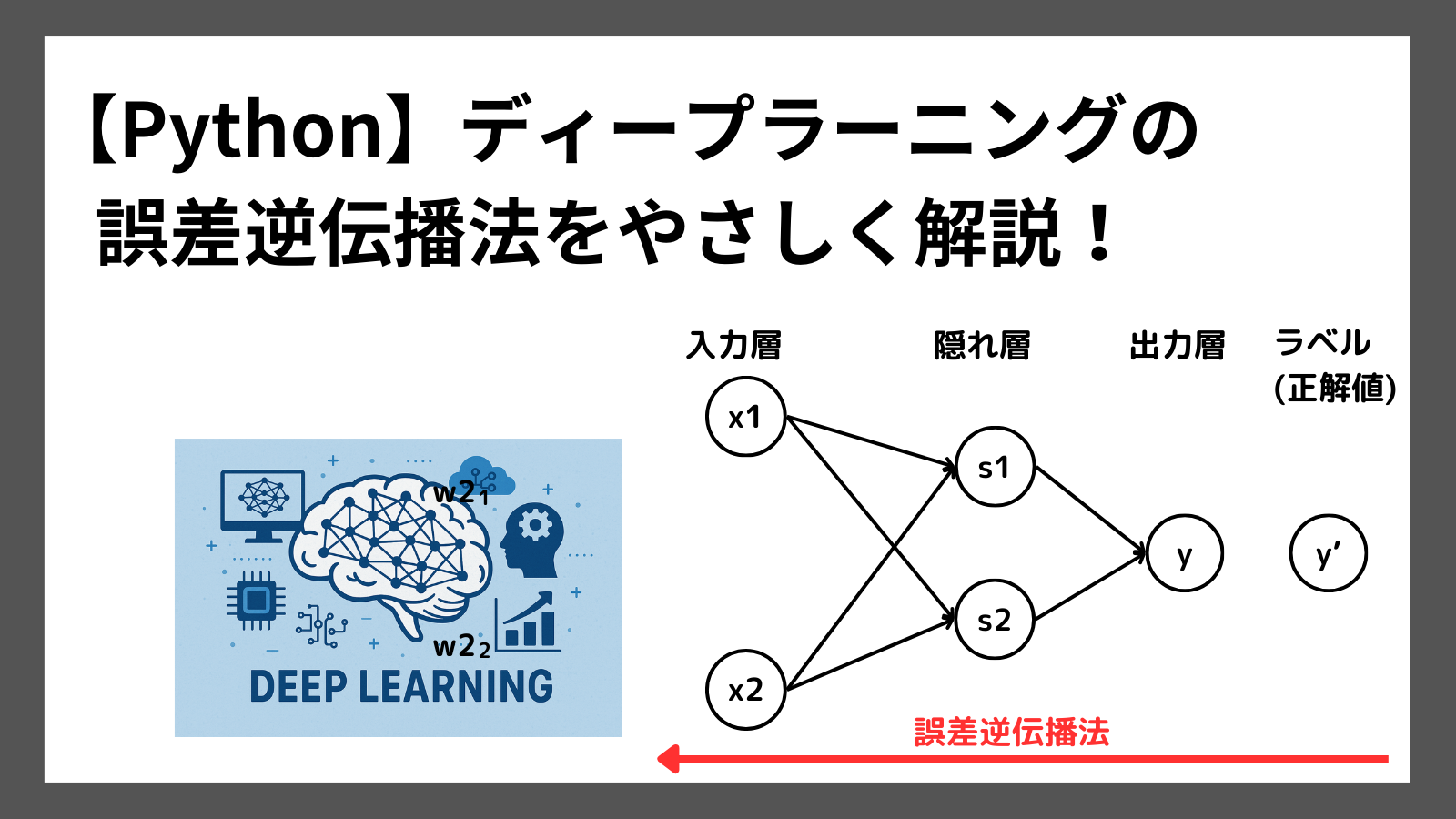
誤差逆伝播法は、出力の誤差を起点に入力方向に向かって「重み」、「バイアス」というパラメータを調整する手法です。
入力から出力に向かってパラメータを調整する方法を「順伝播」といい、出力の誤差から入力に向かって調整することを「逆伝播」といいます。
ニューラルネットワークは、なにより出力が重要です。出力の精度が悪ければ、役に立たないモデルになってしまいます。
そこで、出力の誤差に注目し、出力よりも前の層(隠れ層)にフィードバックをかけて徐々に出力の精度を上げていくために、誤差逆伝播法を用います。
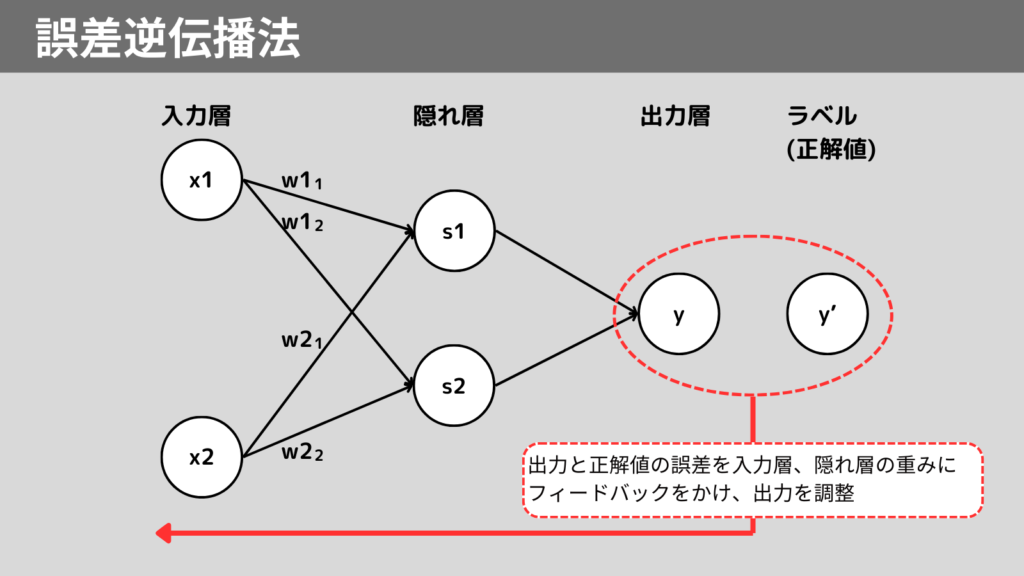
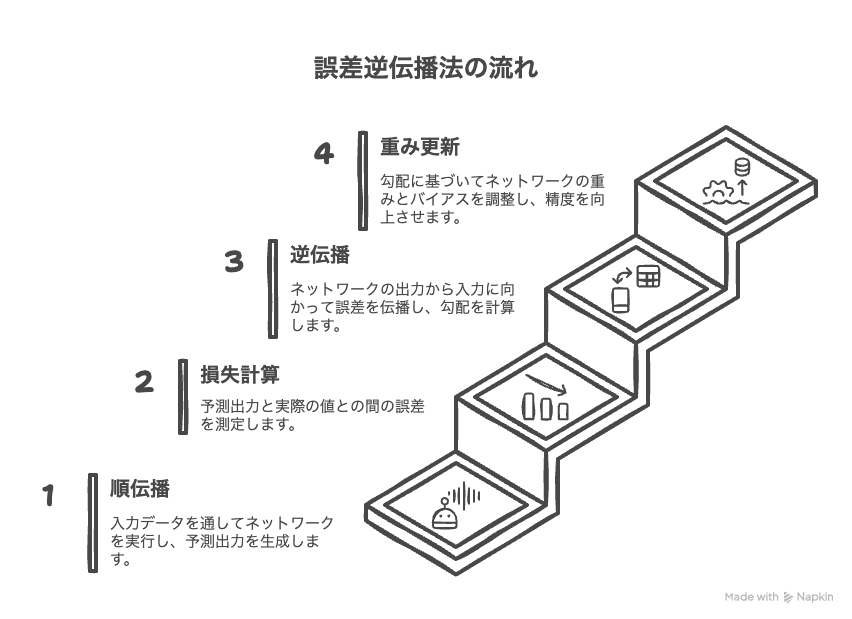
誤差逆伝播法の流れ
誤差逆伝播法のざっくりとした流れは以下の通りです。
- 順伝播
まずは入力から出力までを流し、出力値(予測値)を取得 - 損失関数により誤差の計算
二乗和誤差などの損失関数で出力値(予測値)と正解値の誤差を計算 - 逆伝播
出力から入力に向かって、各層の重み、バイアスに対し、誤差への影響度(損失)を計算(この損失を勾配という) - 重み、バイアスの更新
勾配に基づいて、重み、バイアスを調整
Python実践 誤差逆伝播法
それでは、Pythonを使用し誤差逆伝播法を実装する方法を紹介します。
サンプルコードは以下の通りです。
import numpy as np
# 活性化関数(シグモイド)とその微分
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_deriv(x):
return sigmoid(x) * (1 - sigmoid(x))
# 入力データ(XOR問題)
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]]) # XORの正解
# 初期重みの設定(ランダム)
np.random.seed(0)
W1 = np.random.randn(2, 2) # 入力層 → 隠れ層
b1 = np.zeros((1, 2))
W2 = np.random.randn(2, 1) # 隠れ層 → 出力層
b2 = np.zeros((1, 1))
# 学習率
lr = 0.1
# 学習ループ
for epoch in range(10000):
# --- 順伝播 ---
z1 = X @ W1 + b1
a1 = sigmoid(z1)
z2 = a1 @ W2 + b2
a2 = sigmoid(z2) # 出力
# --- 損失(平均二乗誤差) ---
loss = np.mean((a2 - y) ** 2)
# --- 逆伝播 ---
d_loss_a2 = 2 * (a2 - y)
d_a2_z2 = sigmoid_deriv(z2)
d_z2_W2 = a1
d_loss_W2 = d_z2_W2.T @ (d_loss_a2 * d_a2_z2)
d_loss_b2 = np.sum(d_loss_a2 * d_a2_z2, axis=0, keepdims=True)
d_z2_a1 = W2
d_loss_a1 = (d_loss_a2 * d_a2_z2) @ d_z2_a1.T
d_a1_z1 = sigmoid_deriv(z1)
d_z1_W1 = X
d_loss_W1 = d_z1_W1.T @ (d_loss_a1 * d_a1_z1)
d_loss_b1 = np.sum(d_loss_a1 * d_a1_z1, axis=0, keepdims=True)
# --- 重み・バイアス更新 ---
W2 -= lr * d_loss_W2
b2 -= lr * d_loss_b2
W1 -= lr * d_loss_W1
b1 -= lr * d_loss_b1
print("最終出力:")
print(a2.round(3))実行結果
最終出力:
[[0.025]
[0.499]
[0.97 ]
[0.502]]入力 、正解値、予測値を整理すると以下の通りです。
| 入力1 | 入力2 | 正解値 | 予測値 |
|---|---|---|---|
| 0 | 0 | 0 | 0.025 |
| 0 | 1 | 1 | 0.499 |
| 1 | 0 | 1 | 0.97 |
| 1 | 1 | 0 | 0.502 |
正解値が1に対し、予測値0.499となっているため、予測精度があまり良くないといえます。
まとめ
誤差逆伝播法の仕組みを簡単な図を使って紹介しました。
誤差逆伝播法は、出力と正解値の誤差から重みやバイアスといったパラメータを調整し、最終的な予測精度を高める手法です。
また、Pythonで誤差逆伝播法を実装する方法を紹介しました。
コードは少し長いですが、具体的な実装イメージがついたかと思います。
みなさんの学習の少しでも助けになれば幸いです。
ここまで読んでくださりありがとうございます。