今回は、カテゴリカルなデータ間に対し、関連性を測る方法を紹介します。
連関係数という指標を用いて、カテゴリカルなデータの関連性を測ります。
はじめに
連関係数という指標を使用し、カテゴリカルなデータ間の関連性を測ります。
以下ステップで連関係数を求めます。
それぞれのステップを詳しく説明していきます。
クロス表の作成
クロス表とはなにか、Pythonでクロス表を作成する方法を紹介します。
クロス表とは
クロス表とは、以下のような2つ以上のカテゴリカルなデータをマトリックスで表現したものです。
行と列の交点に、それぞれのカテゴリデータに対応するデータ数が記載されています。
以下は年齢層ごとの好きな映画ジャンルです。
| 年齢層 | アクション | コメディ | ドラマ | ホラー |
|---|---|---|---|---|
| 10-20歳 | 200 | 150 | 50 | 100 |
| 21-30歳 | 180 | 170 | 80 | 70 |
| 31-40歳 | 160 | 130 | 110 | 50 |
| 41歳以上 | 140 | 120 | 130 | 10 |
Pythonでクロス表を作成する方法
それではPythonでクロス表を作成する方法を紹介します。
クロス表を作成するには、pandasのpd.crosstab()を使用します。
pd.crosstab()の使い方は以下です。
pd.crosstab(index, columns)
index: クロス表の行となる配列またはシリーズ
columns: クロス表の列となる配列またはシリーズ
pd.crosstab()のサンプルコードを紹介します。
今回は、tipsのデータセットを使用します。
tipsは、機械学習の分野でサンプルデータとして使用されるレストランのお会計に関するデータセットです。
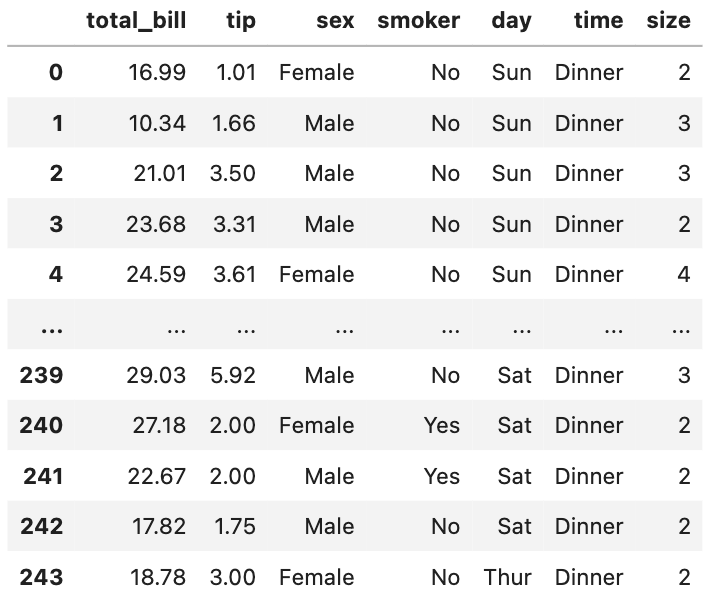
tipsのデータフレームからdayとtimeのクロス表を作成してみましょう!
import pandas as pd
import seaborn as sns
# データの準備
df = sns.load_dataset('tips')
# 'day'と'time'のクロス表を作成
cross_table = pd.crosstab(df['day'], df['time'])
cross_table実行結果
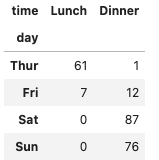
indexにday、columnにtimeが入っています。
火曜日はLunchのお客様がメインであることが見て取れますね!
カイ二乗を算出
続いてはカイ二乗とはなにか、Pythonでカイ二乗を算出する方法を紹介します。
カイ二乗とは
\( \chi^2 \)(カイ二乗)とは、観測されたデータが期待したデータとどれくらい離れているかを測定するために使用されます。
2つのデータが関連しているかしていないか、独立性を評価できます。
カイ二乗は以下計算式で表されます。
\[ \chi^2 = \sum_{i=1} \frac{(O_i – E_i)^2}{E_i} \]
\( O_i \): 観測データ
\( E_i \): 期待度数
Pythonでカイ二乗を算出する方法
Pythonでカイ二乗を算出する方法を紹介します。
カイ二乗を算出するにはSciPyのstatsモジュールのstats.chi2_contingency()を使用します。
stats.chi2_contingency()の使い方は以下です。
stats.chi2_contingency(observed, correction)
引数
observed: クロス表(分割表)
correction: 補正の有無
戻り値
chi2: カイ二乗
p: p値
dof: 自由度
expected: 期待度数の行列
stats.chi2_contingency()のサンプルコードは以下の通りです。
先ほど求めたtipsのデータセットのdayとtimeのクロス表を使用します。
import pandas as pd
import seaborn as sns
from scipy import stats
# データの準備
df = sns.load_dataset('tips')
# 'day'と'time'のクロス表を作成
cross_table = pd.crosstab(df['day'], df['time'])
# カイ二乗を算出
chi2, p, dof, expected = stats.chi2_contingency(cross_table, correction=False)
print(chi2)実行結果
217.11267284348531つ目の戻り値にカイ二乗が入っています。
これでカイ二乗を算出することができました。
連関係数の算出
連関係数とはなにか、Pythonで連関係数を算出する方法を紹介します。
連関係数とは
連関係数は簡単に言うと、カイ二乗を標準化したものです。
変数間の関係を0〜1の範囲で表現されます。
1に近い場合、変数間の関連が強く、0に近い場合は変数間の関連はほとんどない、といえます。
連関係数を式で表すと以下の通りです。
\[ V = \sqrt{\frac{\chi^2}{(\min(a, b)-1) N}} \]
\(\chi^2 \): カイ二乗
a, b: クロス表の行数、列数
min(a, b): aとbの小さい方の数値
\( N \): 観測データの総数
Pythonで連関係数を算出する方法
最後に連関係数を算出する方法を紹介します。
連関係数を算出するには、実際に計算式を作成する必要があります。
では早速、先ほど求めたカイ二乗を使用し、連関係数を算出してみましょう。
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
# データの準備
df = sns.load_dataset('tips')
# 'day'と'time'のクロス表を作成
cross_table = pd.crosstab(df['day'], df['time'])
# カイ二乗を算出
chi2, p, dof, expected = stats.chi2_contingency(cross_table, correction=False)
# 連関係数の計算式で使用する値の準備
N = len(df['day']) # 観測データ数
min_ab = min(cross_table.shape) - 1 # クロス表の行列数の小さいほうからマイナス1
# 連関係数を算出
V = np.sqrt(chi2 / (min_ab * N))
print(V)実行結果
0.9432953070188531連関係数が1に近いので、dayとtimeは関係性が強いことがわかります。
まとめ
今回は、以下ステップで連関係数を求める方法を紹介しました。
- クロス表を作成
- \( \chi^2 \)(カイ二乗)を算出
- \(\chi^2\)(カイ二乗)を標準化し、連関係数を算出
カテゴリカルデータに対し、関係性を知りたいときに連関係数は使用します。
ここまで読んでくださりありがとうございます。
参考
おすすめ教材
米国データサイエンティストが教える統計学超入門講座【Pythonで実践】他のUdemyの講座が気になる方はこちら