今回は、統計学でよく使用されるカイ二乗検定について、Pythonを使用し、実践する方法を紹介します。
動画で詳しく学習したい方はこちらもおすすめ
カイ二乗検定とは
カイ二乗検定は、観測されたデータと期待されるデータ間の違いを検定するための方法です。
特にカテゴリーデータの分析に使用されます。
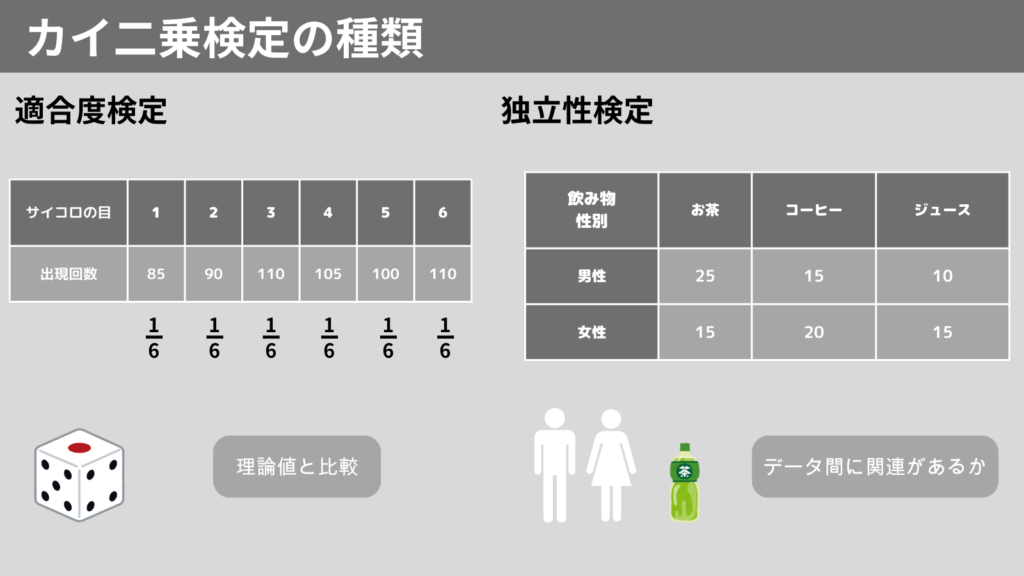
カイ二乗検定の種類
カイ二乗検定には、主に以下2種類があります。
- 適合度検定
– 観測されたデータがある理論と一致しているか
例)サイコロの目が公平に出現するか - 独立性検定
– 2つのカテゴリーデータに関連があるか
例)性別の好きな飲み物の関係
Pythonによるカイ二乗検定の実践
それでは、Pythonを使用し、カイ二乗検定をしていきましょう!
適合度検定と独立性検定をそれぞれ紹介します。
適合度検定
適合度検定は、観測されたデータがある理論と一致するかを検定します。
例: サイコロの目の公平性の検定
サイコロを600回振って各目の出た回数が、均等(各目が100回ずつ)であることを検定します。
この場合、以下仮説を設定します。
- 帰無仮説: サイコロの各目は均等に出現する
- 対立仮説: サイコロの各目は均等に出現しない
import numpy as np
from scipy import stats
# 観測データ(各目の出現回数)
observed = np.array([85, 90, 110, 105, 100, 110])
# 期待値(理論的な均等分布)
expected = np.array([100, 100, 100, 100, 100, 100])
# カイ二乗検定の実行
chi2_stat, p_value = stats.chisquare(observed, expected)
print(f"カイ二乗統計量: {chi2_stat:.4f}")
print(f"p値: {p_value:.4f}")実行結果
カイ二乗統計量: 5.5000
p値: 0.3579この結果p値が有意水準(0.05)より大きいので、帰無仮説は棄却できません。
つまり、このサイコロは公平性に欠けるとは言い切れない結果となりました。
独立性検定
独立性の検定は、2つのカテゴリーデータに関連があるかを検定します。
例: 性別と好きな飲み物の関係を検定
100人にアンケートを取り、性別と好みの飲み物(コーヒー、お茶、ジュース)を調査
このとき、以下仮説を設定します。
- 帰無仮説: 性別と好みの飲み物に関連がない
- 対立仮説: 性別と好みの飲み物に関連がある
import numpy as np
import pandas as pd
from scipy import stats
# データの作成
data = {
'性別': ['男性'] * 50 + ['女性'] * 50,
'飲み物': ['コーヒー'] * 20 + ['お茶'] * 15 + ['ジュース'] * 15 +
['コーヒー'] * 15 + ['お茶'] * 25 + ['ジュース'] * 10
}
df = pd.DataFrame(data)
# クロス集計表の作成
contingency_table = pd.crosstab(df['性別'], df['飲み物'])
print("クロス集計表:")
print(contingency_table)
# カイ二乗検定の実行
chi2, p_value, dof, expected = stats.chi2_contingency(contingency_table)
print(f"\nカイ二乗統計量: {chi2:.4f}")
print(f"p値: {p_value:.4f}")
print(f"自由度: {dof}")実行結果
クロス集計表:
飲み物 お茶 コーヒー ジュース
性別
女性 25 15 10
男性 15 20 15
カイ二乗統計量: 4.2143
p値: 0.1216
自由度: 2この結果p値が有意水準(0.05)より大きいので、帰無仮説は棄却できません。
つまり、性別によって好みの飲み物に関連があるとは言い切れない結果になりました。
カイ二乗検定の注意点
カイ二乗検定は、データの関連を調べるために便利な手段です。
ですが、カイ二乗検定を実施するうえで注意点がいくつかあります。
- サンプルサイズ
小さいサンプルサイズでは、結果が信頼できない可能性がある
大きすぎるサンプルサイズでは、統計的に有意であっても、実質的な意味がない場合がある - 独立性の仮定
各観測データは独立している必要がある - 因果関係の推論
カイ二乗検定はデータ間の関連を示すだけで、因果関係を示しているわけではない
まとめ
カテゴリーデータを分析する際に使用するカイ二乗検定を紹介しました。
カイ二乗検定は主に以下の2種類あり、それぞれの検定を実際にPythonで実施する方法を説明しました。
- 適合度検定 stats.chisquare()
- 独立性検定 stats.chi2_contingency()
ここまで読んでくださりありがとうございます。
参考
おすすめ教材
米国データサイエンティストが教える統計学超入門講座【Pythonで実践】他のUdemyの講座が気になる方はこちら