今回は、クロージャについて紹介します。
クロージャは、外側の関数の引数を保持する関数のことです。
これだけだとわからないと思うので、Pythonのコードを交えて、具体的に説明していきます。
| 目的 | 講座名 | 到達点 | レベル/前提 | 想定時間 | こんな人に | 評価 |
|---|---|---|---|---|---|---|
| 現場志向でPython×DSを通しで習得 | 米国データサイエンティストがやさしく教えるデータサイエンスのためのPython講座 | Python基礎〜NumPy/Pandas/ Matplotlib/Seaborn、 Docker+JupyterLabでの環境構築までハンズオン | 初心者〜初級(Mac推奨/軽いプログラミング経験があると◎) | 24時間 | Pythonの基礎固めは完了し、ステップアップをしたいかた | |
| 広く一式を“ブートキャンプ”形式で学ぶ | 【世界で55万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜 | 統計・Python(Numpy/Pandas)〜機械学習(scikit-learn/TensorFlow)・可視化・Tableauまで網羅 | 初心者OK | 26時間 | データサイエンスとは何をする職業なのか知りたいかた | |
| AI/機械学習の入門(Colab対応・数学やさしめ) | みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2025年最新版】 | Python基礎+機械学習の基本(文字認識・株価分析などの小プロジェクト)をColabで体験 | 超初心者〜初級(中学数学レベルで可) | 10時間 | 手を動かしてAIを学習したいかた |
クロージャとは
クロージャには、以下の特徴があります。
- 関数内関数
- 関数の戻り値に関数内関数を定義
- 外側の関数の状態を持った関数
実際のコードを見て解説します。
def outer(a, b):
def inner():
c = a + b
return c
return inner
f = outer(1, 2)
print(f())クロージャの特徴① 関数内関数
関数outer()の内で、関数inner()が定義されています。
このinner()関数のように、関数内で定義されている関数を関数内関数といいます。
クロージャの特徴② 外側の関数の戻り値に関数内関数を設定
外側の関数の戻り値(return文)に関数内関数を設定します。
今回の例では、innerをreturn文に設定しています。
このときのinner関数には()をつけないことに注意してください!
戻り値には、inner関数のオブジェクトをセットしたいためです。
クロージャの特徴③ 外側の関数の状態を持った関数
3つ目のクロージャの特徴は、今までの2つの特徴よりも少し難しいです。
外側の関数の状態を持つとは、簡単にいうと、
外側の関数が呼ばれたときの、引数の情報を保持するということです。
これだけでは、わかりにくいと思うので、次章にてクロージャの動きと合わせて説明します。
クロージャの動き
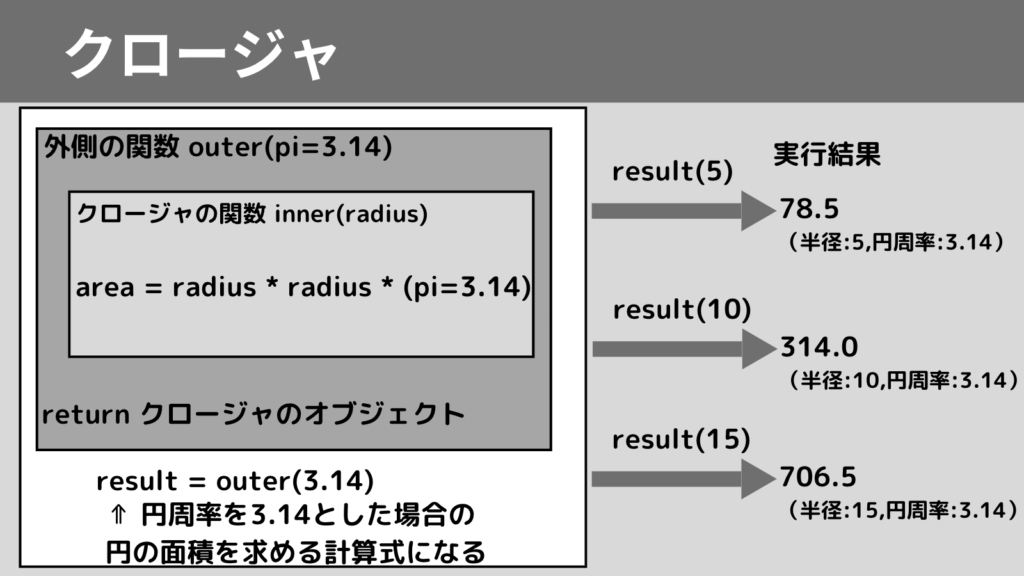
以下のコードは、円の面積を求めるクロージャを実装したコードです。
外側の関数がcalc_areaで、クロージャがcalc関数にあたります。
外側の関数calc_areaは、円周率piを引数とし、
クロージャのcalc関数を戻り値としています。
一方で、クロージャcalc関数は、円の半径radiusを引数として、
円の面積を計算した結果を戻り値にしています。
result1〜3の変数には、それぞれの円周率で円の面積を求めるオブジェクトが格納されています。オブジェクトというと難しいかもしれませんが、
それぞれの円周率ごとに円の面積を求めることができる箱ができたイメージです。
あとは、半径を引数として指定すれば、それぞれの円周率で円の面積が求められます。
def calc_area(pi):
def calc(radius):
area = radius * radius * pi # 円の面積=半径x半径x円周率
return area
return calc
result1 = calc_area(3.14159) # pi = 3.14159
result2 = calc_area(3.14) # pi = 3.14
result3 = calc_area(3) # pi = 3
radius = 10 # 半径 10とする
print(result1(radius)) # radius = 10, pi = 3.14159 のときの円の面積
print(result2(radius)) # radius = 10, pi = 3.14 のときの円の面積
print(result3(radius)) # radius = 10, pi = 3 のときの円の面積実行結果
314.159
314.0
300それぞれの円周率で、円の面積を求めた計算結果が表示されました。
クロージャのメリット
クロージャの使い方がわかったところで、なぜクロージャを使うのか気になると思います。
なので、クロージャのメリットについて、紹介します。
クロージャのメリットは、状態を保持したまま、違う処理を実行できる点です。
上で紹介したコードをみてください。
result1〜3で外側の関数calc_areaに対し、
それぞれの円周率piを引数とした実行結果を保持しています。
この実行結果を保持したresult1〜3に対し、
半径radiusを指定して、円の面積を求めることができます。
半径radiusは、サンプルでは、10を指定していますが、変更も可能です。
このようなクロージャのメリットが、
クロージャの3つ目の特徴「外側の関数の状態を持った関数」に相当します。
まとめ
クロージャについて紹介しました。
クロージャの特徴は以下の通りです。
- 関数内関数
- 関数の戻り値に関数内関数を定義
- 外側の関数の状態を持った関数
クロージャは外側の関数の状態を保持しながら、別の関数として処理ができるので便利です。
これまで読んでくださりありがとうございます。