【Python】F検定で等分散性の検定をする方法を解説

2024年10月13日2024年10月16日

URLをコピーしました！

今回はデータの等分散性を検定するために使用される、F検定について解説します。

また、Pythonを使用し、実際にF検定を実施する方法も紹介します。

F検定とは

F検定(F-test)は、等分散性を検定する手法です。

等分散性とは、データのばらつき具合が等しいという性質のことを指します。

F分布という確率分布を使用し、2つの分散の比率を検定します。

F分布についてはのちほど詳しく説明します。

F検定を実施するときの仮説設定は、基本的に以下です。

帰無仮説: 2つのデータの分散は等しい
対立仮説: 2つのデータの分散は異なる

F値

F値(F-statistic)は、F検定で使用される統計量です。

2つの分散の比率を表す統計量であり、計算式は以下の通りです。

$$ F = \frac{{s_1}^2}{{s_2}^2} $$

${s_1}^2$: 母集団1の不偏分散 ${s_2}^2$: 母集団2の不偏分散

F分布を用いて、このF値どれだけ有意であるかを検定するのがF検定です。

F分布

続いてはF分布について説明します。

F分布はカイ二乗分布に従う変数の比を用いて以下のように定義されます。

$$ F = \frac{\frac{{\chi_1}^2}{d_1}}{\frac{{\chi_2}^2}{d_2}} $$

$\chi_1^2, \chi_2^2$: カイ二乗

$d_1, d_2$: 自由度

自由度はサンプル数$n$を用いると、以下のように表現できます。

$$ F = \frac{\frac{1}{n_1-1}\chi_1^2}{\frac{1}{n_2-1}\chi_2^2} $$

PythonでF検定実践

それでは、F検定をPythonを用いて実践していきましょう！

serbonのデータセットであるtipsを用います。

土曜日と日曜日でtotal_billの分散に差があるかを見てみましょう。

PythonでF分布を描画するためには、Scipyのstatsモジュールの以下を使用します。

stats.f(dfn, dfd).sf(f)

dfn: 分子の自由度 dfd: 分母の自由度 f: F値

stats.f(dfn, dfn)でF分布を描画しています。

sf(f)で指定したF値からの面積を求めています。

図で表すと以下です。

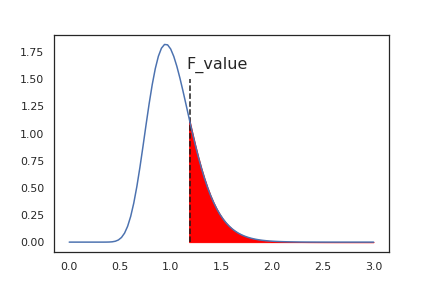
サンプルコードは以下の通りです。

import seaborn as sns
from scipy import stats

# データセットをロード
df = sns.load_dataset('tips')

#　土曜日の合計金額
sat_tips = df[df['day']=='Sat']['total_bill']
#　日曜日の合計金額
sun_tips = df[df['day']=='Sun']['total_bill']

# データサイズ
n1 = len(sat_tips)
n2 = len(sun_tips)
# 自由度
dfn = n1 - 1
dfd = n2 - 1
# 不偏分散
var1 = stats.tvar(sat_tips)
var2 = stats.tvar(sun_tips)

# F値の計算
f_value = var1 / var2
print(f"F値: {f_value:.4f}")

# F検定
f_test = stats.f(dfn=dfn, dfd=dfd).sf(f_value)
print(f"p値: {f_test:.4f}")

実行結果