今回は、教師あり学習の基本である回帰分析および線形回帰について紹介します。
動画で詳しく学習したい方はこちらもおすすめ
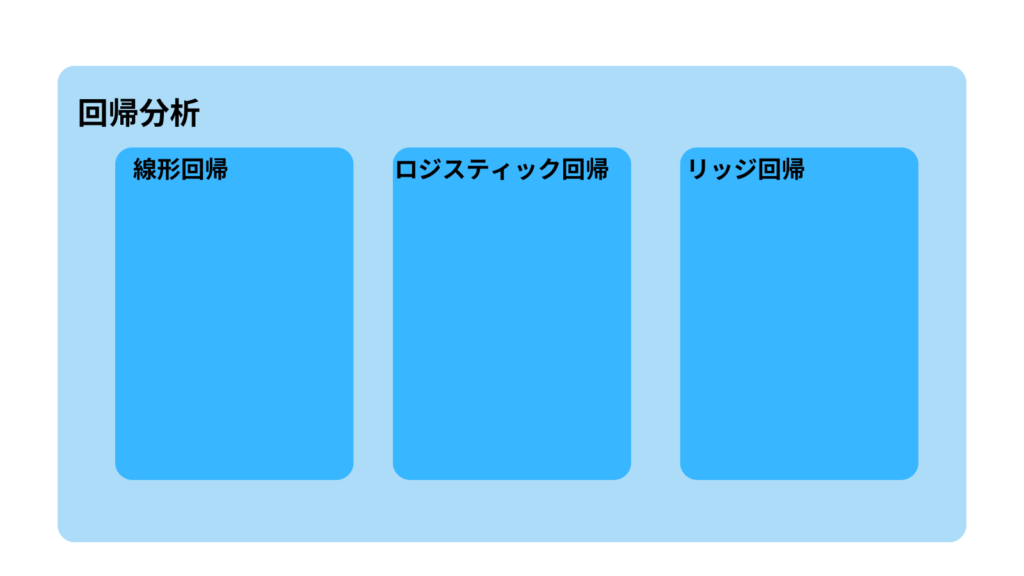
回帰分析とは
回帰分析とは、説明変数と目的変数の関係をモデル化し、予測または推定するための統計的手法です。
説明変数とは、予測に使用する要因。目的変数とは、予測したい結果のことをいいます。
また、回帰分析の種類には、以下があります。
- 線形回帰
- ロジスティック回帰
- リッジ回帰
この回帰分析のなかから、最も基本である線形回帰について詳しく説明していきます。
線形回帰とは
線形回帰とは、回帰分析の一種で、説明変数と目的変数の関係が線形であると仮定し、分析を行うことです。
既知のデータを使用し、未知のデータを予測します。
既知のデータ( 正解ラベル)を用いて、学習することから教師あり学習に当てはまります。
線形回帰の種類
線形回帰には、以下の種類があります。
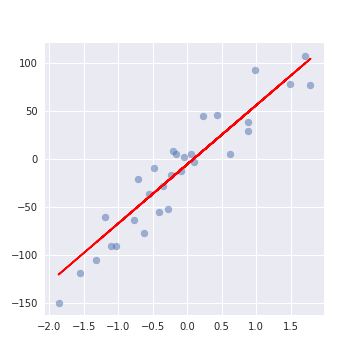
- 単回帰 ひとつの説明変数を使用、2次元で表現される
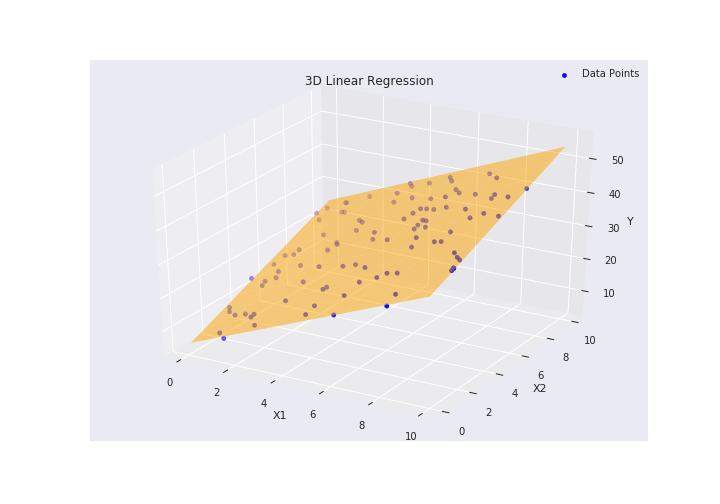
- 重回帰 複数の説明変数を使用、3次元以上で表現される
それぞれを図で表すと以下の通りです。
左が単回帰で、右が重回帰です。
単回帰は2次元であり、重回帰が3次元であることがわかると思います。
数学的表現
単回帰と重回帰の数式を紹介します。
難しくはないので、数式のほうが理解しやすい方もいるかと思います。
単回帰と重回帰を数式で表すと以下の通りです。
単回帰
$$ y = w_{1}x + b $$
\(y\): 目的変数 \(x\): 説明変数 \(w\): 傾き \(b\): 切片
目的変数\(y\)に対し、説明変数\(x\)がひとつであることが、式からもわかります。
重回帰
$$ y = w_{1}x_{1} + … + w_{n}x_{n} + b $$
\(y\): 目的変数 \(x_{i}\): 説明変数 \(w_{i}\): 回帰係数 \(b\): 切片
重回帰は、目的変数\(y\)に対し、説明変数\(x_i\)が複数あります。
メリット・デメリット
線形回帰のメリット・デメリットは以下の通りです。
| メリット | シンプルさと解釈のしやすさ 説明変数と目的変数の関係を直感的に理解できる |
| 計算効率が良い 計算コストが安く、大規模データにも適応する | |
| デメリット | 非線形関係への対応の限界 変数間の関係が非線形の場合、汎化性能が悪いことがある |
| 外れ値の影響 外れ値に敏感、予測精度に影響を及ぼす |
Python実践 線形回帰
それでは、Pythonで線形回帰を実装する方法を紹介します。
# 必要なライブラリのインポート
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# データセットを準備
X, y = make_regression(random_state=3, n_features=1, noise=20, n_samples=30)
# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# モデルの作成
lr = LinearRegression()
# 訓練データでモデルの学習
lr.fit(X_train, y_train)
# モデルの評価
print("Test score: {:.2f}".format(lr.score(X_test, y_test)))
# グラフを表示
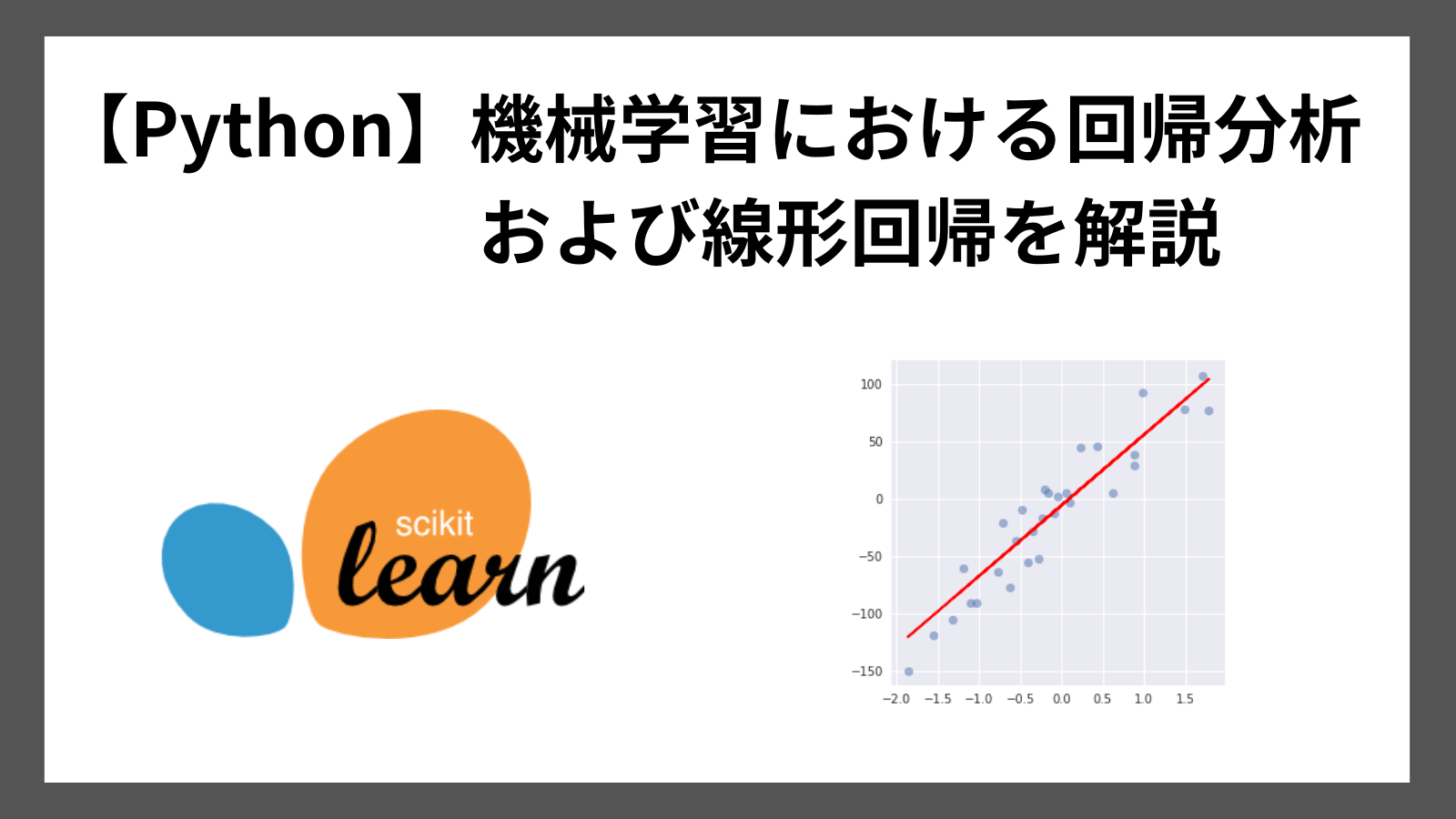
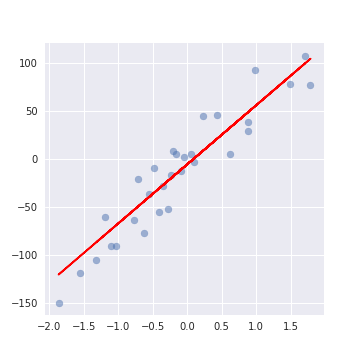
plt.figure(figsize=(5, 5))
plt.scatter(X, y, alpha=0.5)
plt.plot(X, lr.predict(X), color='r')
実行結果
まとめ
回帰分析と線形回帰を紹介しました。
線形回帰は機械学習における最も基本的なアルゴリズムです。
データの関係から直線を引くだけなので、直感的で理解しやすいと思います。
ここまで読んでくださりありがとうございます。