【Python】正規分布を作成する方法

2024年5月3日2024年6月21日

URLをコピーしました！

今回は、統計学で最も使用する分布図である正規分布について紹介します。

正規分布とは

正規分布(Normal Distribution)は統計学で最も使用される確率分布です。ガウス分布とも呼ばれます。

正規分布は以下の式で表されます。

\[ f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]

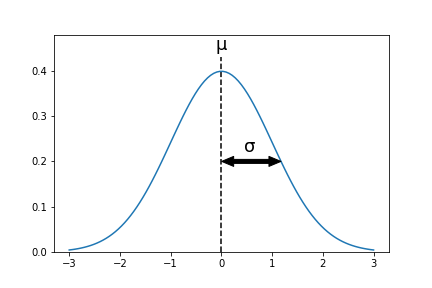
平均\(\mu\)(ミュー)と標準偏差\(\sigma\)(シグマ)の2つのパラメータによって値が決まります。

平均\(\mu\)は分布の位置、標準偏差\(\sigma\)は分布の幅に対応しています。

このことから正規分布は\(N(\mu, \sigma^2)\)と表記されることもあります。

また、平均0, 標準偏差1 すなわち\(N(0, 1)\)のときの正規分布を標準正規分布といいます。

正規分布を作成

それではPythonで正規分布を作成する方法を紹介します。

正規分布を作成するには、SciPyのstatsモジュールを使用します。

使い方は以下の通りです。

normが正規分布、pdfが確率密度関数を表しています。

stats.norm.pdf(x, loc, scale)

x: 確率変数
loc: 平均
scale: 標準偏差

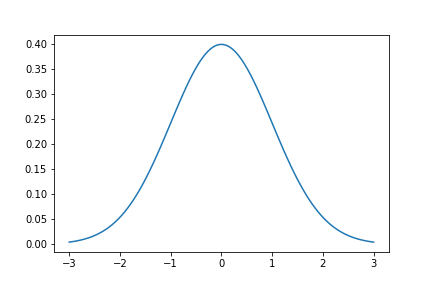
標準正規分布 \(N(0, 1)\) を作成してみましょう。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 確率変数の準備
x = np.linspace(-3, 3, 100)
# yに正規分布の値を格納
y = stats.norm.pdf(x, loc=0, scale=1)

# 正規分布を描画
plt.plot(x, y)

実行結果

パラメータの変更

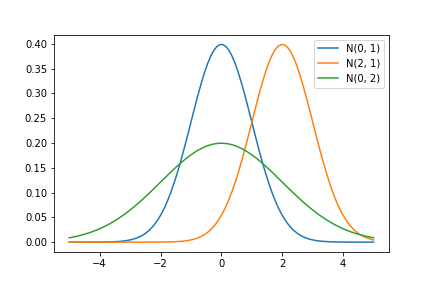
平均\(\mu\)と標準偏差\(\sigma\)を変更してみて、グラフがどのように変化するのか見てみましょう。

以下3パターン作成してみます。

\(N(0, 1)\)
標準正規分布
\(N(2, 1)\)
平均\(\mu\)を変更したパターン
\(N(0, 2)\)
標準偏差\(\sigma\)を変更したパターン

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 確率変数の準備
x = np.linspace(-5, 5, 100)

# N(0, 1)標準正規分布
y1 = stats.norm.pdf(x, loc=0, scale=1)
# 正規分布を描画
plt.plot(x, y1, label="N(0, 1)")

# N(2, 1)平均μを変更したパターン
y2 = stats.norm.pdf(x, loc=2, scale=1)
# 正規分布を描画
plt.plot(x, y2, label="N(2, 1)")

# N(0, 2)標準偏差σを変更したパターン
y3 = stats.norm.pdf(x, loc=0, scale=2)
# 正規分布を描画
plt.plot(x, y3, label="N(0, 2)")
# 凡例の表示
plt.legend()

実行結果