【Python】確率分布を作成する方法

今回は、Pythonで確率分布を作成する方法を紹介します。

確率分布とは

確率分布とは、ある事象で発生する確率がどのように分布しているかを表すものです。

確率分布には離散型確率分布と連続型確率分布があります。

それぞれをグラフで表すと、以下の通りです。

左が離散型確率分布、右が連続型確率分布です。

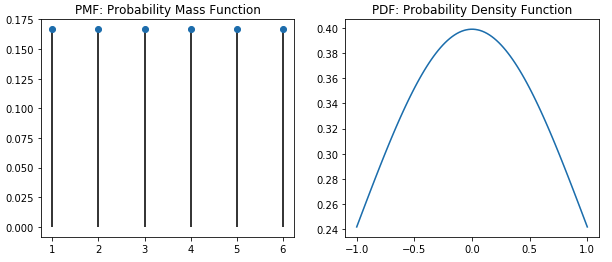
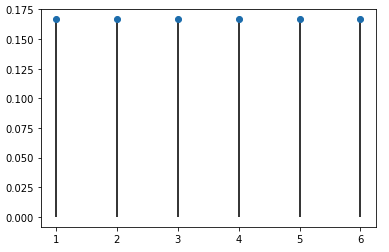
離散型確率分布を作成

確率質量関数(PMF: Probability Mass Function)を使用して、各確率変数の確率を表しています。

確率質量関数(PMF)は離散的な値(一般的には整数)に対し、その値が発生する確率を与える関数です。

一様分布を使用し、離散型確率分布を作成してみます。

一様分布の離散型確率分布をPythonで作成するにはSciPyのstatsモジュールのstats.randint.pmf()を使用します。

stats.randint.pmf()の使い方は以下です。

low: 分布の下限
high: 分布の上限(この値を含まない)
k: 確率を求めたい値

サンプルコードは以下の通りです。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 確率変数の準備 整数1〜6
x = np.arange(1, 7)
# xに対し、確率質量関数から求めた確率をyに格納
y = stats.randint(1, 7).pmf(x)
# x, yをプロット
plt.plot(x, y, 'o')
# 0-yまでに縦線を引く
plt.vlines(x, 0, y)

実行結果

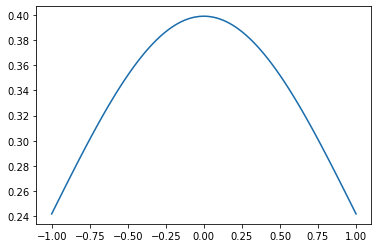
連続型確率分布を作成

確率密度関数(PDF:Probability Density Function )を使用して、各確率変数の確率を表しています。

確率密度関数(PDF)は連続的な値の範囲から確率を求めるために使用される関数です。

ある範囲内の確率はその範囲における確率密度関数の積分により求めることができます。

正規分布を使用し、連続型確率分布を作成してみます。

正規分布の連続型確率分布を作成するには、SciPyのstatsモジュールのstats.norm.pmf()を使用します。

stats.norm.pmf()の使い方は以下です。

x: 確率変数
loc: 平均
scale: 標準偏差

連続型確率分布をPythonで表示するサンプルコードは以下です。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 確率変数の準備 -1〜1まで値を100コ
x = np.linspace(-1, 1, 100)
# xに対し、確率密度関数から求めた確率をyに格納
y = stats.norm.pdf(x, loc=0, scale=1) # 平均0, 標準偏差1
# x, yをプロット
plt.plot(x, y)

実行結果

まとめ

今回は確率分布を離散型と連続型に分けて、Pythonで表示する方法を紹介しました。

以下方法で、確率分布を作成しました。

ここまで読んでくださりありがとうございます。

参考

おすすめ教材

他のUdemyの講座が気になる方はこちら

Pythonで学ぶあたらしい統計学の教科書 第2版

¥3,630 （2024/04/08 23:55時点 | Amazon調べ）

楽天市場

ポチップ